
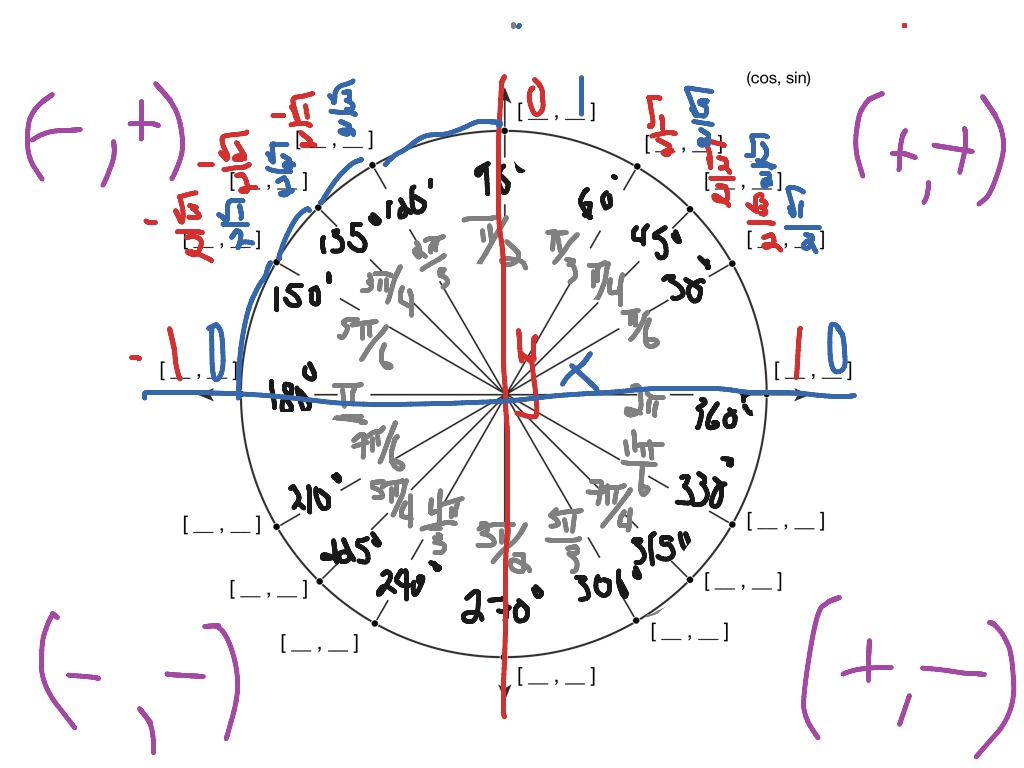
Once you master all the values for the first quadrant of the unit circle, you have mastered the entire diagram. What Is the Easiest Way to Memorize the Unit Circle? Finally, join each of the angles (from steps 2 and 3) to the origin. For this set, you can find the positions by creating the 30-60-90-degree special triangle in the first quadrant and mirroring the value to corresponding angles in the other quadrants. Repeat step 2 for these points, labeling them by angle and position coordinates. Next, divide the circle again, so it now has 12 equal parts. Once you find a position, use the charge values to fill in the other 3 corresponding points in the 2nd, 3rd, and 4th quadrants. Your calculations should give you the following coordinate (√2/2, √2/2). Use the basic trigonometric identities to solve the x and y values of the triangle. This gives you a 45-45-90-degree special triangle. For example, for the 45° angle, draw a perpendicular line from the point the 45° angle line touches the circle to the x-axis. You can draw special triangles for each of these angles to determine each point’s (x, y) coordinates. Typically, the positive direction is anticlockwise, and you can label the angles in degrees or radians (or both, one inside the circle and the other outside). Label these angles at the point where the lines meet the unit circle. Step 2: Divide the Circle by Eightįrom the origin, divide the unit circle into 8 equal parts to create more angles. Mark the points where the circle intersects with the axes from the end closest to your right hand in an anticlockwise direction as 0° (1,0), 90° (0,1), 180° (-1,0), 270° (0, -1).
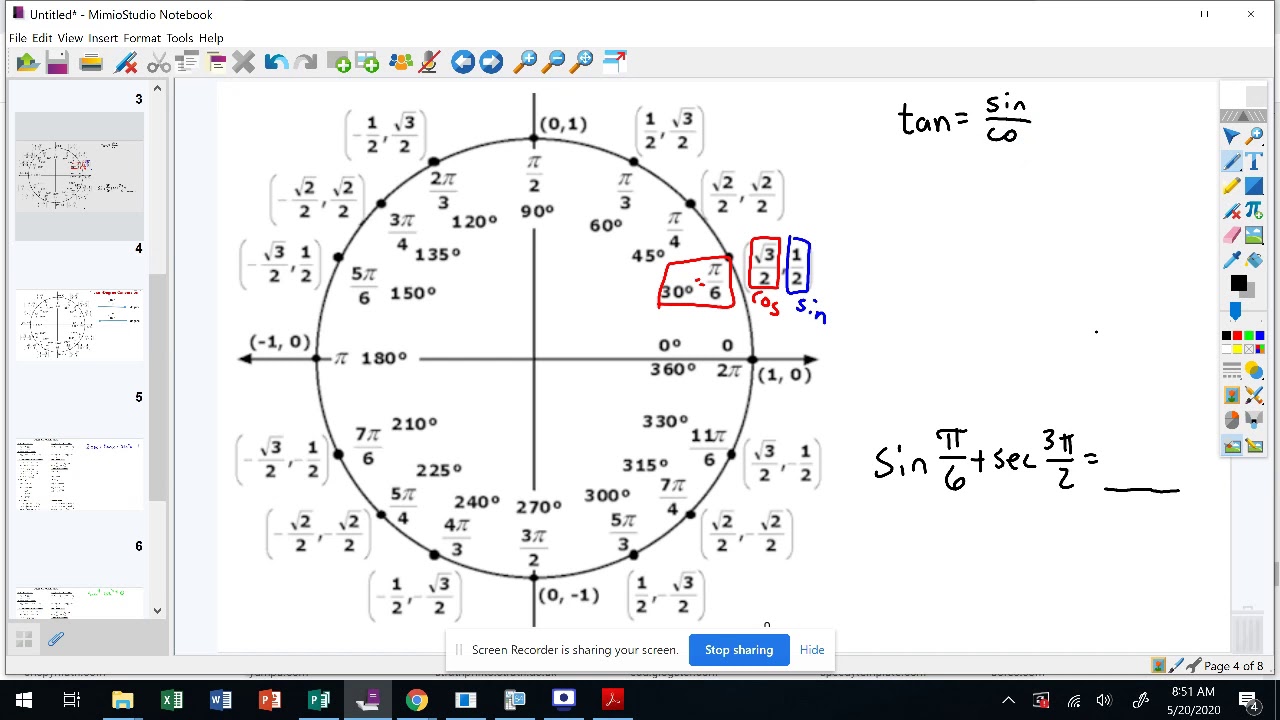
Next, draw a horizontal and vertical line through the origin to the points of the circle and label them the x and y axes. The exact measurement of the radius will depend on how small or large you would like your circle to be, as long as you mark it as one unit. Measure a radius of one unit from this point and use it to draw a circle. On a Cartesian plane, allot a point (0,0) that will be the origin and center of the unit circle. $\,1\,$ (inclusive), since it's a point on the unit circle.Note: The position of the points in a unit circle is obtained by dividing the circle into 8 and 12 parts and reading the coordinates from the corresponding special triangles. Notice immediately that both coordinates are always numbers between $\,-1\,$ and
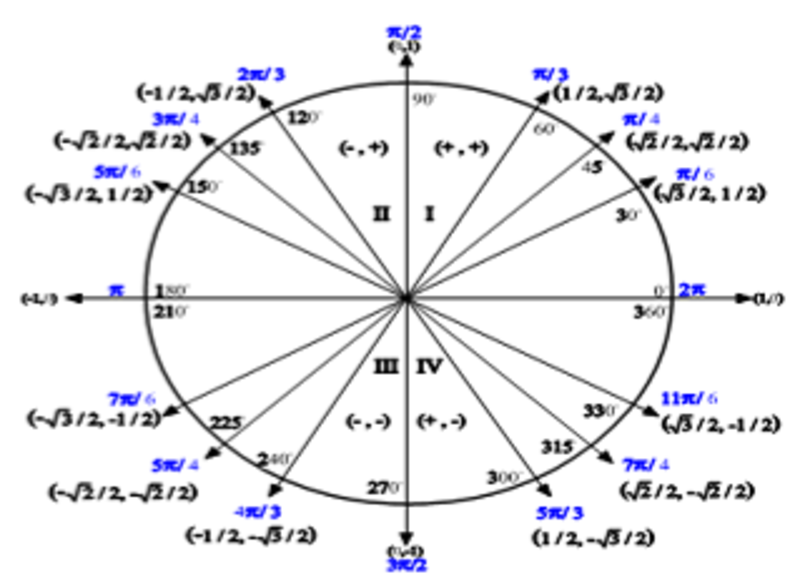
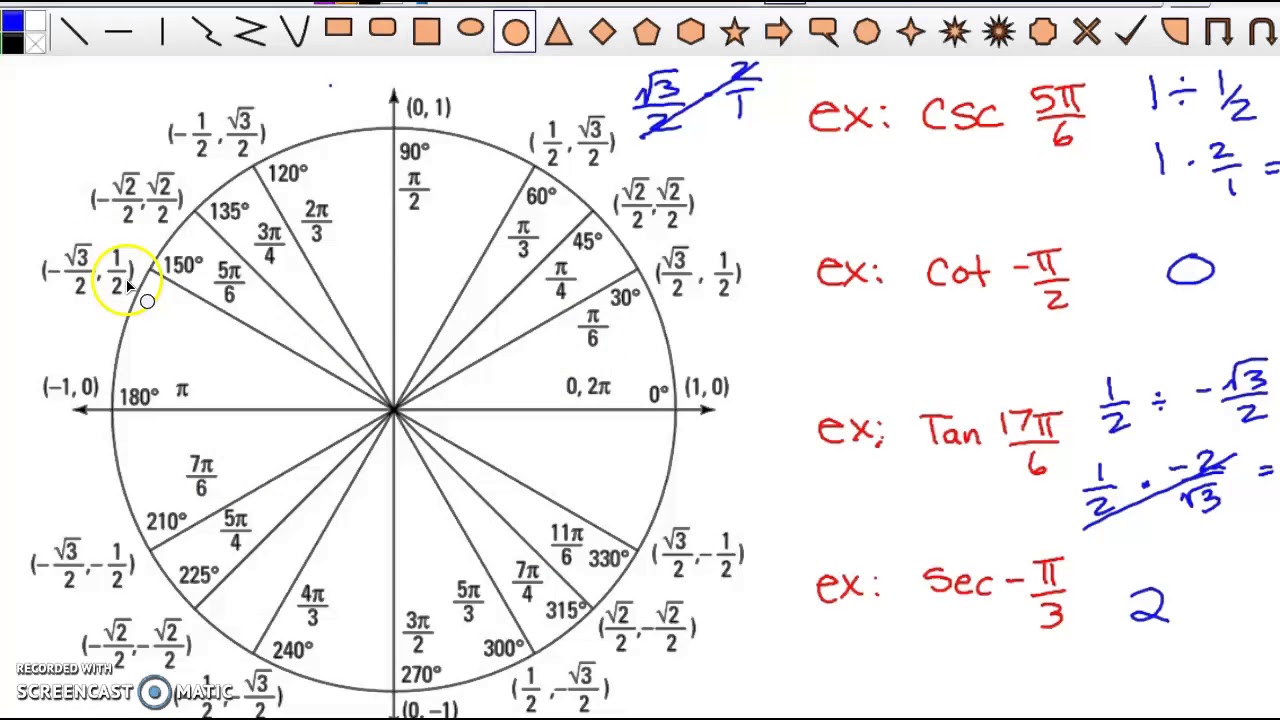


 0 kommentar(er)
0 kommentar(er)
